

About us
We are a theoretical research group at the School of Electrical and Electronic Engineering and the Institute for Digital Molecular Analytics and Science at Nanyang Technological University, Singapore. The group is lead by Assistant Professor Matthew R. Foreman.
Our research focuses on optical and plasmonic sensing, polarisation sensitive imaging, disordered media and electromagnetic theory. More information on some of our past and present projects can be found by visiting our Research pages.
Recent news

Two papers accepted!
24 Sep 2025: Congratulations to Kaiyuan Wang, our PhD student, who had two of his papers accepted today. The first article introduces an approach to design high order EPs using transformation optics principles and was accepted in Laser & Photonics Reviews. The second article, co-authored with Niall Byrnes, was accepted in Optics Letters and discusses how our earlier work on Generalized Wigner Smith perturbation theory can be generalised to account for degenerate systems.
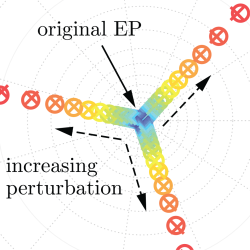
New arXiv preprint
11 Aug 2025: We have a new preprint out on arXiv! Our paper, "Generalized Wigner-Smith theory for perturbations at exceptional and diabolic point degeneracies," introduces a new residue-based perturbation theory to understand and predict how non-Hermitian systems respond to external changes. We believe this offers a powerful framework for precision tuning and inverse design.

New PhD Student - Duong Le Dang
4 Aug 2025: As we start a new academic year OTG is joined by a new member, Duo. Although new to his PhD, Duo is not new to the group having previously worked with us as a Global Connect+ Fellow. He has however now graduated from Hanoi University of Science and Technology with his BSc in Electronic and Telecommunication Engineering and come back to Singapore, where his project will be looking at modelling and informatic optimisation of optical imaging and sensing devices.
Paper published in Newton
Recent publications
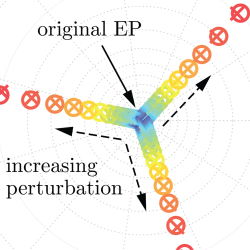
Abstract : Spectral degeneracies, including diabolic (DP) and exceptional (EP) points, exhibit unique sensitivity to external perturbations, enabling powerful control and engineering of wave phenomena. We present a residue-based perturbation theory that quantifies complex resonance splitting of DP and EP type spectral degeneracies using generalized Wigner–Smith operators. We validate our theory using both analytic Hamiltonian models and numerical electromagnetic simulations, demonstrating excellent agreement across a range of cases. Our approach accurately predicts degenerate resonance splitting using only scattering data, offering a powerful framework for precision tuning, inverse design, and practical exploitation of non-Hermitian phenomena.

Abstract : Exceptional points (EPs) in non-Hermitian photonic systems have attracted considerable research interest due to their singular eigenvalue topology and associated anomalous physical phenomena. These properties enable diverse applications ranging from enhanced quantum metrology to chiral light-matter interactions. Practical implementation of high order EPs in optical platforms however remains fundamentally challenging, requiring precise multi-parameter control that often exceeds conventional design capabilities. This work presents a novel framework for engineering high order EPs through transformation optics (TO) principles, establishing a direct correspondence between mathematical singularities and physically controllable parameters. Our TO-based paradigm addresses critical limitations in conventional Hamiltonian approaches, where abstract parameter spaces lack explicit connections to experimentally accessible degrees of freedom, while simultaneously providing full-field mode solutions. In contrast to prevailing parity-time-symmetric architectures, our methodology eliminates symmetry constraints in EP design, significantly expanding the possibilities in non-Hermitian photonic engineering. The proposed technique enables unprecedented control over EP formation and evolution in nanophotonic systems, offering new pathways for developing topological optical devices with enhanced functionality and robustness.

Abstract : Perturbing resonant systems causes shifts in their associated scattering poles in the complex plane. In a previous study [arXiv: 2408.11360], we demonstrated that these shifts can be calculated numerically by analyzing the residue of a generalized Wigner-Smith operator associated with the perturbation parameter. In this work, we extend this approach by connecting the Wigner-Smith formalism with results from standard electromagnetic perturbation theory applicable to open systems with resonances of arbitrary quality factors. We further demonstrate the utility of the method through several numerical examples, including the inverse design of a multi-layered nanoresonator sensor and an analysis of the enhanced sensitivity of scattering zeros to perturbations.
Funding
Our research is supported by generous funding from:



